
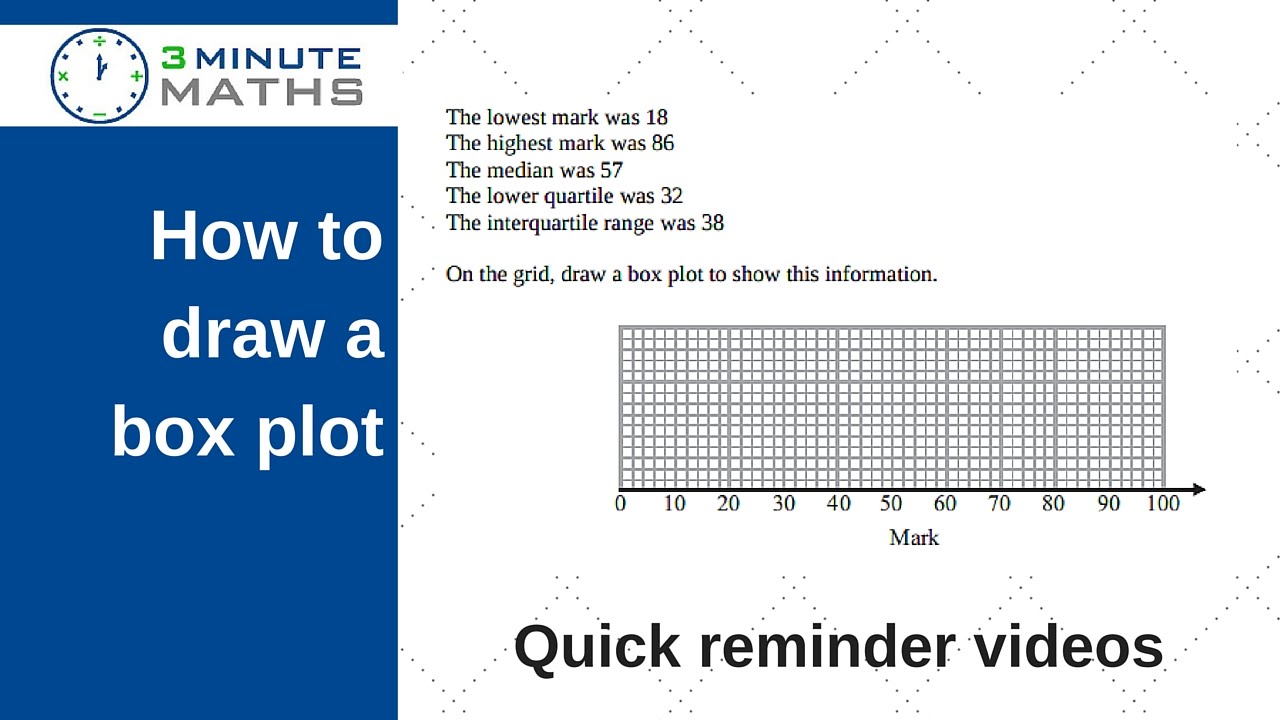
To be precise, if n is even, the sequence splits nicely into halves, so there's no problem: we find the median of the lower half. However, we again have to take n's parity into account. It's the median of the lower half of the entries. On the other hand, if n is even, we need to take the average of the two middle numbers, i.e., median = (a n/2 + a (n+2)/2) / 2. If n is odd, there is indeed such an entry, and we have median = a (n+1)/2. We need to find the value with the same number of entries to the left (i.e., smaller) and to the right (i.e., larger). In the ordered sequence, it is minimum = a₁. In our case, the entries are ordered, so we have maximum = aₙ. That is because it's usually easier to calculate the five numbers in the order given below.
Box and whisker plot calculator how to#
Also, note that below, the subsequent steps on how to make a box-and-whisker plot are in a different order to those in the above section. If they weren't, we'd have to order them before we do anything else. For simplicity, let's assume that they are listed from least to most. Say that you have a sequence of numbers a₁, a₂, a₃. Therefore, explaining how to find them seems like a reasonable thing to begin with, don't you think? What is more, we'll also go through the whole thing the other way round, i.e., explain how to read a box-and-whisker plot.Īs mentioned in the above section, the box-and-whisker plot calculator is basically a tool to visualize five values associated with a dataset. For now, we'll focus on general instructions and formulas, which we then apply to a numerical example in the dedicated section. On the plot, it's the bottom dark blue line.Īlright, now that we know what a box plot is and can identify its components, it's time to see how to make a box-and-whisker plot in practice. The opposite of the maximum: it marks the smallest entry of the dataset. On the graph, it's the bottom side of the box. Together with the third quartile, it forms the interquartile range, i.e., the box on the box-and-whisker plot example above, which shows where roughly half of the entries are. Similar to its equivalent from point 2., it marks the end of the range in which one-fourth of the values lie. In the picture, it's the light blue line in the middle. It's not the same as the mean, mind you! Instead, it says that half of the entries are larger and the other half are smaller than the median. On the plot, it's the top side of the box. Formula-wise, it's the median of the top half of the values. As such, the third quartile marks the end of the range in which three-fourths of the entries lie. On the graph, it's the top dark blue line.Ī quartile is one-fourth of the dataset. Simple enough: it's the largest entry in the dataset.
It's time to learn what they are from top to bottom. The bunch is called the five-number summary of a dataset, and sure enough, Omni's box-and-whisker plot maker provides their values together with the graph itself. In essence, the five horizontal lines are all there is to it. Let's look at a box-and-whisker plot example and explain its components. It is most often used to analyze large sequences of numbers where we don't care much what the individual values are but would rather see where most of them fall, and how far from that the extreme values are. A box plot (often expanded to a box-and-whisker plot) represents a dataset's distribution.


 0 kommentar(er)
0 kommentar(er)
